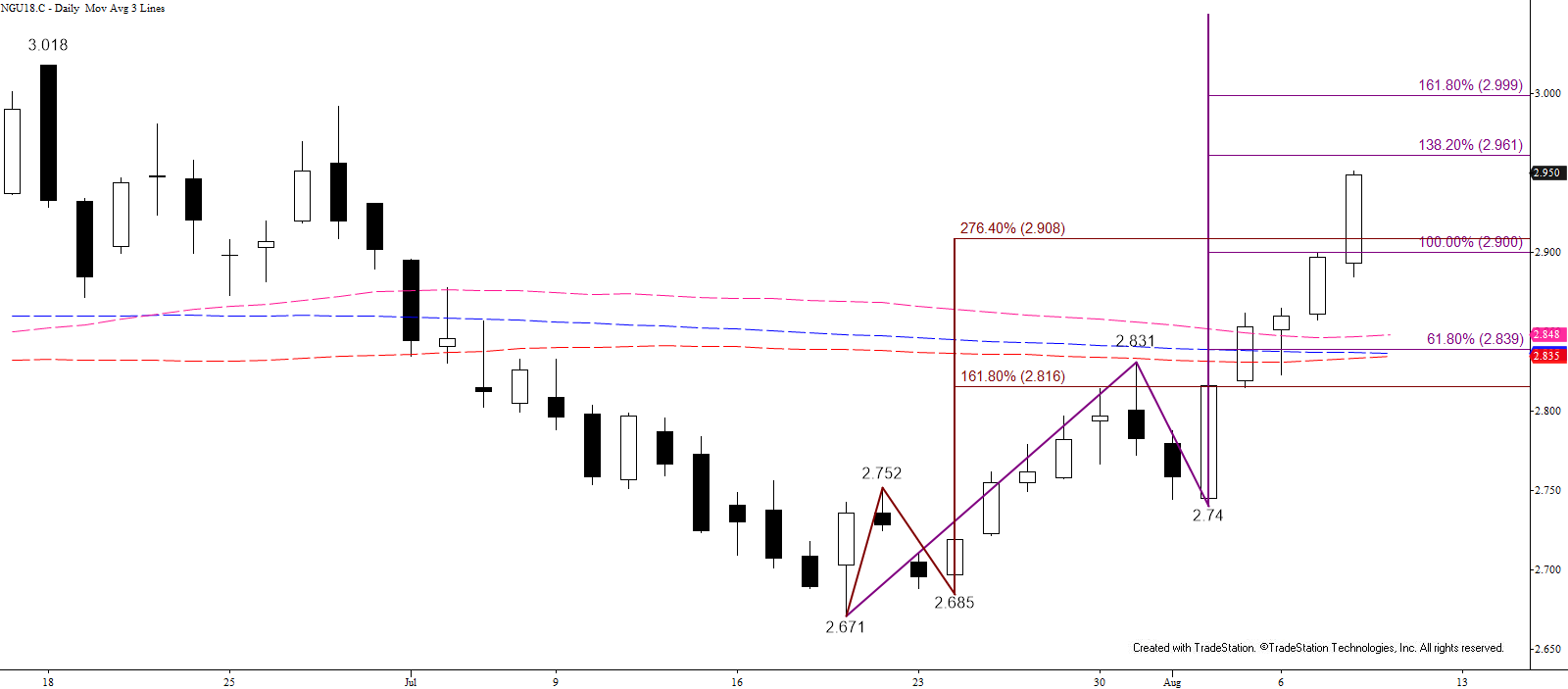
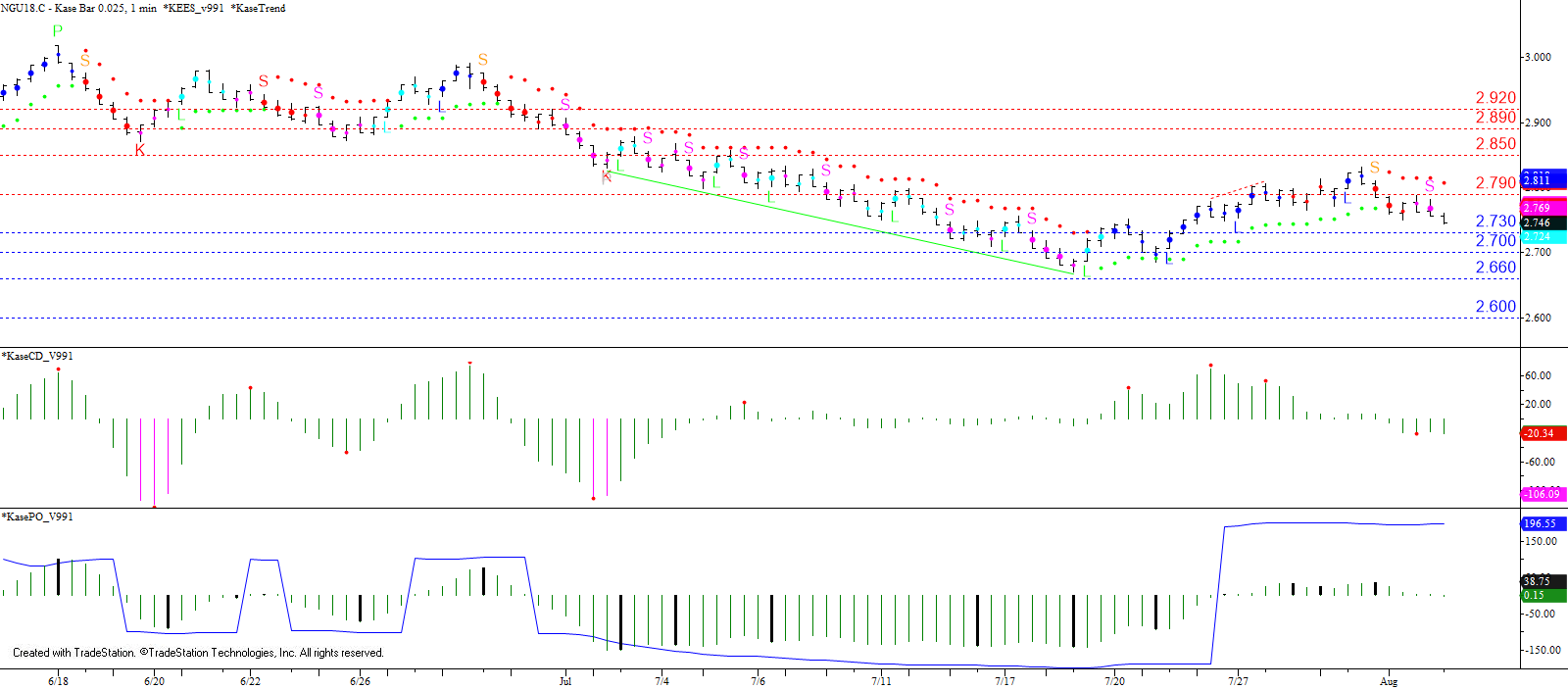
WTI Crude Oil
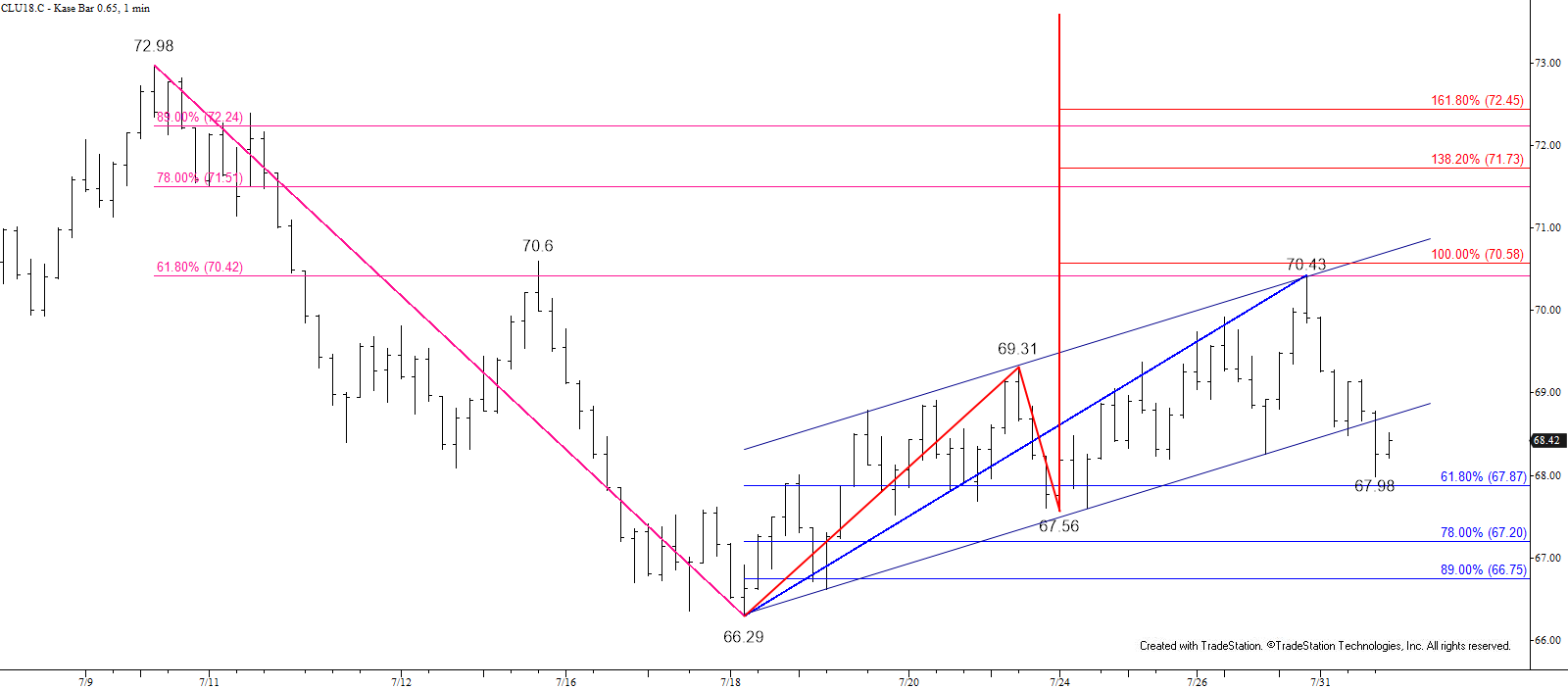
The near-term outlook for WTI crude oil became positive today, and although October did not settle above $69.8 it rose above that level late this afternoon. There is a lot of resistance near the upper limit of the $69.8 target, right around $70.0 still, so there is an outside chance the move up will stall early tomorrow. However, given today’s surge higher, and because prices have overcome the 62 percent retracement of the decline from $71.4, any pullback will most likely be a corrective buying opportunity for bulls while today’s $68.4 midpoint holds.
The next objective is $70.4 and a close above this would call for $70.9 and eventually the next major objective of $71.5. This is the last target protecting October WTI’s $71.63 swing high. Therefore, settling above $71.5 would open the way for a new high of at least $72.0 this week.
Immediate support is $69.3 and key support for tomorrow is $68.4, which should hold. Settling below $68.4 would suggest today’s move up was based on weak external factors that could not support the move up. In that case, look for prices to challenge $67.9 and possibly the $67.33 intra-day swing low. A move below the latter would invalidate the wave up from $66.86 and shift odds to be solidly back in favor of a continued decline.
Brent Crude Oil
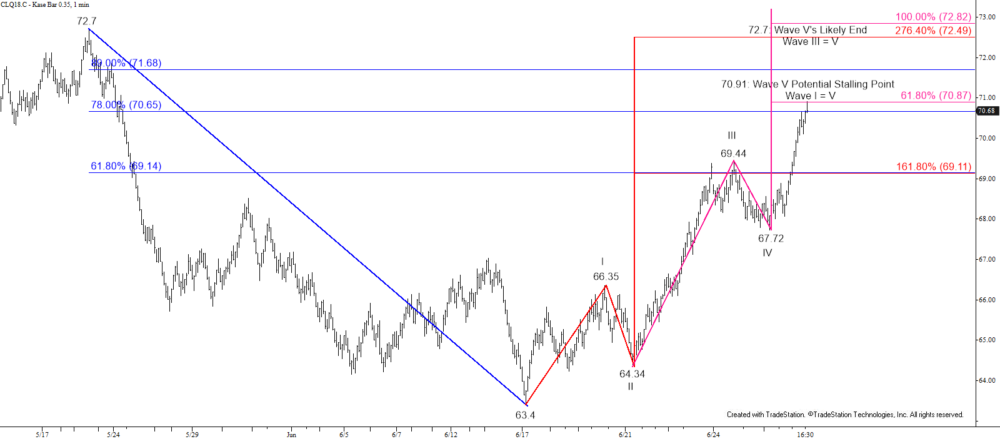
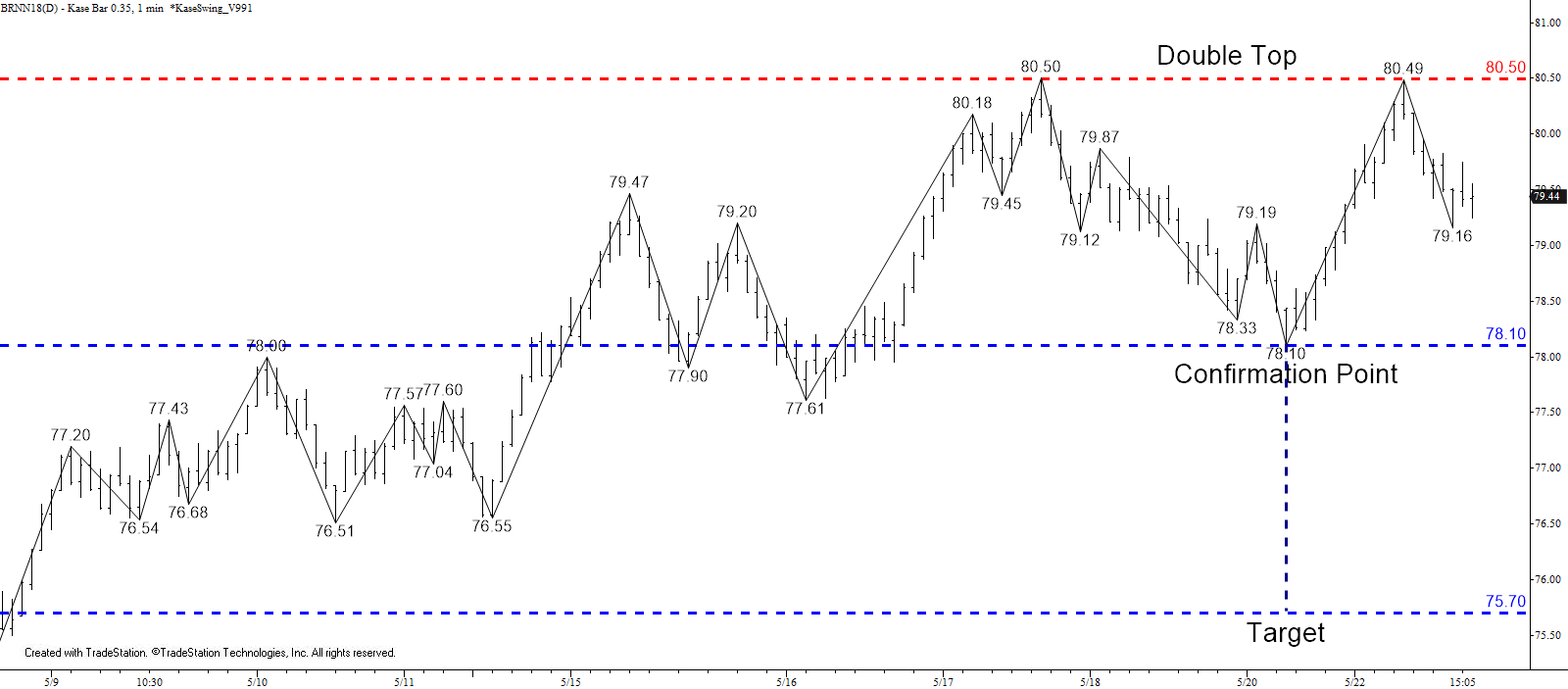
Brent’s move up accelerated again today and the pattern up from $75.64 has unfolded as a five-wave formation that met its Wave V targets at $79.54 this afternoon. The move up is poised to continue and $79.9 and likely $80.5 should be challenged tomorrow.
That said, because the five-wave pattern met its target at $79.54 a corrective pullback might take place first. Such a move is expected to hold support at today’s $78.2 midpoint, which means the pullback will be a buying opportunity. However, a close below $78.2 would suggest the move up has stalled again and that another major test of support will take place over the next few days. Given today’s rise, this is doubtful.
This is a brief analysis for the next day or so. Our weekly Crude Oil Forecast and daily updates are much more detailed and thorough energy price forecasts that cover WTI, Brent, RBOB Gasoline, Diesel, and spreads. If you are interested in learning more, please sign up for a complimentary four-week trial.